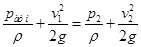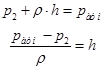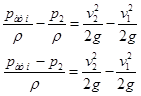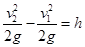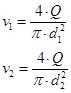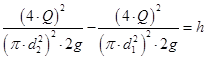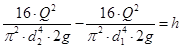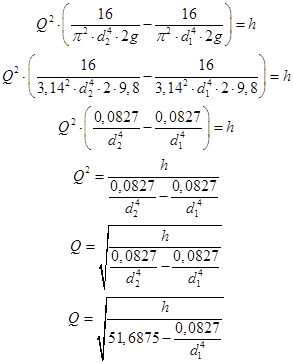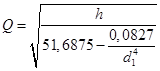Определить массовый расход воздуха через сопло аэродинамической трубы

Содержание

Расчет расхода сжатого воздуха через сопло
ЗАДАЧА 3. определение расхода воздуха через сопло центробежного вентилятора
Аэродинамика
Введение
Глава 1. Кинематика сплошной среды
Глава 2. Основные уравнения аэродинамики
Глава 3. Аэродинамическое подобие
Глава 4. Течение газов с большими скоростями
Глава 5. Пограничный слой
Глава 6. Аэродинамические характеристики профиля
Глава 7. Аэродинамические характеристики крыла
Глава 8. Аэродинамические характеристики оперения и рулей
Глава 9. Механизация
Глава 10. Аэродинамические характеристики тел вращения
Глава 11. Аэродинамические характеристики воздушных винтов
Глава 12. Аэродинамические характеристики самолета
Глава 13. Влияние аэродинамических характеристик
на безопасность полетов
Глава 14. Влияние аэродинамических характеристик
на экономичность полетов
Ответы к задачам
Стандартная атмосфера

Расчет расхода сжатого воздуха через сопло

Иногда возникает потребность в подсчете количества (объема) сжатого воздуха, которое выйдет через отверстие (сопло) определенного диаметра в атмосферу, или в иной объем с атмосферным давлением, за какой-либо промежуток времени. Это может быть нужно для подсчета объема утечек, или, с некоторыми поправками, для расчета потребления сжатого воздуха оборудованием.

Следует отметить, что задача расчета объемного расхода газа, будь то сжатый воздух или ной газ, через отверстие (сопло), хотя и может на первый взгляд показаться тривиальной, на самом деле далеко не так проста. Пропускная способность сопла в значительной степени зависит как от характеристик (прежде всего, геометрии) самого сопла, так и от «окружения», в том числе геометрии и других характеристик подводного трубопровода и входа/выхода сопла. В случае с оборудованием, как правило, расход газа, требующийся для работы оборудования, обязательно не только рассчитывается производителем этого оборудования теоретически, но и тщательно, многократно и при различных условиях проверяется им опытным путем. Поэтому, получаемый по приведенной ниже формуле расход является приблизительным и может рассматриваться только в качестве ориентировочной цифры.

Итак, массовый расход идеального газа через сопло можно рассчитать по следующей формуле (ознакомиться с последовательностью вывода этой формулы можно на странице http://en.wikipedia.org/wiki/Choked_flow, а также на страницах, на которые ссылается вышеуказанная):

, где
m — искомый массовый расход газа, кг/с
С — поправочный коэффициент по пропускной способности сопла (если не известен, условно принимаем за 1)
A — площадь сечения сопла, м², рассчитывается из его радиуса по формуле A=π·r²
P — абсолютное давление газа перед соплом, Па = Н/м² = кг/(м·с²)
k = cp/cv, (http://en.wikipedia.org/wiki/Specific_heat_capacity)
при этом cp — удельная теплоемкость при постоянном давлении, для воздуха = 29,12 Дж·моль -1 ·K -1
при этом cv — удельная теплоемкость при постоянной температуре, для воздуха = 20,8 Дж·моль -1 ·K -1
то есть k = 1,4
M — молекулярная масса, кг/кмоль. Для сжатого воздуха = 28 кг/кмоль
Z — коэффициент сжимаемости при определенных давлении и температуре. Для сжатого воздуха принимаем за 1 (http://en.wikipedia.org/wiki/Compressibility_factor) .
R — константа идеального газа = 8314,5 (Н·м)/(кмоль·K)
T — температура газа перед соплом, K

После того, как по формуле выше рассчитан массовый расход воздуха, его можно перевести в объемный, разделив полученное значение на плотность воздуха, то есть примерно на 1,2 кг/м³.

Разумеется, если рассчитывался расход через сопло другого газа, то в формуле следует использовать соответствующие характеристикам этого газа величины: удельную теплоемкость, молекулярную массу, коэффициент сжимаемости и, наконец, при переводе полученного значения массового расхода в объемный, плотность.

Источник

ЗАДАЧА 3. определение расхода воздуха через сопло центробежного вентилятора

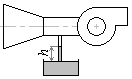
Центробежный вентилятор засасывает воздух из атмосферы через сопло.

К цилиндрической части сопла с диаметром d2=200мм присоединена трубка, опущенная в бак с водой. Высота поднятия воды в трубке h мм.

Определить расход воздуха через сопло (температура воздуха – 15°С, давление – 101,6кПа.

Сечение 2-2 принимаем в цилиндрической части сопла, сечение 1-1 – на входе в сопло, где давление равно атмосферному (Ра=101,6кПа).

Плоскость сравнения совмещаем с осью трубы, тогда

С учетом этого, уравнение Бернулли получим в виде

Определим величину вакуума, обеспечивающего поднятие воды по трубке на высоту h

где d1 – диаметр устья сопла, м

Ответ:

Поможем написать любую работу на аналогичную тему

ЗАДАЧА 3. определение расхода воздуха через сопло центробежного вентилятора

Источник

Аэродинамика

Введение

Изучить материал [1, Введение с. 3 – 7].

-уравнение состояния для совершенного газа

где — давление [Па];

— плотность газа [кг/м3];

Дж/(кг×К) – удельная газовая постоянная;

— температура [К];

-скорость звука в совершенном газе

где = 1,4 – показатель адиабаты, равный отношению теплоемкости при постоянном давлении к теплоемкости при постоянном объеме.

1. Нормальные и касательные напряжения. Динамическое взаимодействие.

2. Газодинамические переменные. Уравнение состояния.

3. Упрощенные физические модели идеального, вязкого и сжимаемого газов.

В1. Определить плотность воздуха, если при давлении 200 кПа его температура равна 30°С.

В2. Определить скорость звука в воздухе при плотности 0,657 кг/м3 и давлении 97500 Па.

В3. Определить температуру воздуха, если его скорость звука равна 427 м/с.

Глава 1. Кинематика сплошной среды

Изучить материал [1, гл. 1, с. 8 – 21].

Вихревое влияние в заданной точке пространства определяется формулами:

-от элемента произвольного вихря определяется уравнением Био-Савара

где — циркуляция скорости по замкнутому контуру ;

— расстояние до исследуемой точки;

— элемент вихря;

-от бесконечного прямолинейного вихря

;

-от полубесконечного прямолинейного вихря

;

-от отрезка прямолинейного вихря

;

-уравнение неразрывности для трубки тока

где — площадь поперечного сечения трубки тока.

5. Задание движения газа по Эйлеру и по Лагранжу.

6. Линия тока. Трубка тока. Поверхность тока.

7. Вихревое течение. Вихревая линия. Вихревая трубка. Вихревая пелена.

8. Интенсивность (напряженность) вихревой трубки. Циркуляция скорости.

9. Теорема Стокса для вихревого течения.

10. Вихревое влияние. Индуцированная скорость.

11. Массовый расход. Уравнение неразрывности.

1.1. В воздухе находится бесконечный, прямолинейный вихрь интенсивностью 100 м2/с. Определить вихревое влияние в исследуемой точке на расстоянии 5 м от вихря.

1.2. В воздухе находится полубесконечный, прямолинейный вихрь интенсивностью 150 м2/с. Определить вихревое влияние в исследуемой точке на расстоянии 7 м от вихря и на расстоянии 10 м от начала вихря (рис. 1.1).

1.3. В воздухе расположены два параллельных бесконечных вихря с интенсивностями соответственно = 100 м2/с и = — 240 м2/с. Расстояние между вихрями 16 м. Определить вихревое влияние в точке, расположенной посередине между вихрями.

1.4. В воздухе расположены два параллельных бесконечных вихря с интенсивностями соответственно = 150 м2/с и = — 320 м2/с. Между вихрями расположена точка, в которой от каждого вихря индуцируются равные по абсолютной величине скорости. Определить вихревое влияние в этой точке, если расстояние между вихрями равно 8 м.

1.5. В воздухе расположен вихрь ab длиной 300 м с интенсивностью 9000 м2/с. Определить скорость, индуцированную в точке c, если расстояния х и y соответственно равны 100 и 80 м (рис. 1.2).

1.6. Определить скорость, индуцированную вихревым кольцом в точке в центре кольца. Радиус кольца равен 0,98 м при циркуляции равной 120 м2/с. (рис. 1.3)

Глава 2. Основные уравнения аэродинамики

Изучить материал [1, гл. 2, с.17 – 44].

-массовый расход для трубки тока

;

-уравнение Бернулли для несжимаемой жидкости

;

-уравнение Бернулли для сжимаемой жидкости

;

-уравнение количества движения

где — равнодействующая поверхностных сил, действующих на выделенный объем трубки тока;

-уравнение момента количества движения

где — равнодействующий момент от моментов поверхностных сил, действующих на выделенный объем трубки тока.

12. Уравнение Навье — Стокса.

14. Уравнение Бернулли для несжимаемого и сжимаемого газов.

15. Критическая точка в потоке. Статическое, динамическое давления и давление торможения.

16. Измерение скорости на борту самолета.

17. Уравнения количества движения и момента количества движения для трубки тока.

2.1. Определить массовый расход воздуха через сопло аэродинамической трубы на земле при стандартных атмосферных условиях, если диаметр входа в сопло равен 2 м, диаметр выхода из сопла 1,2 м, давление на входе в сопло 99000 Па, а давление на выходе из сопла 96000 Па.

2.2. Определить скорость несжимаемого воздушного потока, если давление торможения равно 99500 Па, статическое давление равно 97400 Па при температуре воздуха 12°с.

2.3. Определить силу, действующую на сопло аэродинамической трубы при стандартных атмосферных условиях, если скорость на входе в сопло 11 м/c, диаметр входа в сопло равен 2,2 м, а диаметр выхода из сопла равен 0,8 м.

2.4. Определить крутящий момент, действующий на разбрызгиватель диаметром 1,5 м, если массовый расход равен 1,6 кг/с при скорости истечения жидкости 5 м/с (рис. 2.1).

Глава 3. Аэродинамическое подобие

Изучить материал [1, гл. 3, с. 45 – 65].

— коэффициенты аэродинамических сил

; ; ; ;

— коэффициенты аэродинамических моментов

; ; ; ;

;

-критерии аэродинамического подобия:

— число Маха;

= — число Рейнольдса;

— число Фруда;

— число Струхаля;

где — скоростной напор

— характерный линейный размер;

— коэффиц. динамической вязкости ;

— коэффициент кинематической вязкости ;

— число оборотов в секунду.

18. Проблемы теории аэродинамического подобия.

19. Системы координат в аэромеханике.

20. Аэродинамические силы и моменты.

21. Аэродинамические коэффициенты и коэффициент давления.

22. Критерии подобия: число Маха, число Рейнольдса.

Читайте так же: Не подходит труба нексия

23. Критерии подобия: число Фруда, число Струхаля. Степень турбулентности.

24. Углы атаки и скольжения ЛА.

3.1. Модель самолета продувается в аэродинамической трубе. Какая скорость [м/с] должна быть в рабочей части, чтобы обеспечить подобие по сжимаемости, если натурное число маха равно 0,82, а температура в рабочей части равна 18°с?

3.2. Модель самолета в масштабе 1:20 продувается в аэродинамической трубе. Какая плотность должна быть в рабочей части, чтобы обеспечить подобие по вязкости, если температура в рабочей части равна 5°с, температура и плотность в полете соответственно равны минус 20°с и 0,96 кг/м3?

3.3. Гидросамолет имеет поплавок с площадью миделевого сечения 1,8 м2 и взлетает с воды со скоростью 165 км/ч. С какой скоростью (м/с) надо испытывать геометрически подобную модель поплавка с площадью миделевого сечения 0,31 м2, чтобы обеспечить подобие с учетом весомости воды?

3.4. Самолет летит со скоростью 450 км/ч при числе оборотов винта 1050 об/мин. Какое число оборотов должна иметь модель винта (масштаб 1: 10), чтобы обеспечить кинематическое подобие при скорости 220 км/ч?

Глава 4. Течение газов с большими скоростями

Изучить материал [1, гл. 4, с. 66 – 94].

— связь газодинамических переменных с параметрами торможения и числом Маха

; ; ,

где индекс 0 относится к параметрам торможения;

где индекс * относится к критическим параметрам;

— массовый расход газа через сверхзвуковое сопло

;

— интенсивность скачка уплотнения

25. Изоэнтропические одномерные течения газа.

27. Влияние сжимаемости на трубку тока.

28. Слабые возмущения и скачки уплотнения.

29. Интенсивность скачка уплотнения и коэффициент восстановления давления.

4.1. Определить температуру торможения в форкамере аэродинамической трубы, если в рабочей части получена скорость 650 м/с при статической температуре 8°С.

4.2. Определить плотность торможения в форкамере аэродинамической трубы, если в рабочей части получена скорость 720 м/с при статической температуре равной 12°С и статическом давлении 3,66×104 Па.

4.3. Определить массовый расход воздуха через сверхзвуковое сопло аэродинамической трубы, если диаметр критического сечения равен 0,2 м, критическая скорость равна 300 м/с при плотности торможения 2 кг/м3.

4.4. Определить критическую скорость воздуха в сверхзвуковом сопле аэродинамической трубы, если температура торможения равна минус 5°с.

4.5. Определить статическое давление за косым скачком уплотнения, имеющим угол наклона 32 градуса при числе Маха полета 2,25 на высоте 12000 м.

Глава 5. Пограничный слой

Изучить материал [1, гл. 5, с. 95 – 119].

Справочные сведения Таблица 1

Характеристики пограничного слоя

Толщина пограничного слоя

Коэффициент трения плоской пластины

при

-коэффициент трения смешанного пограничного слоя на пластине

где — коэффициент сопротивления турбулентного трения пластины при числе Рейнольдса, вычисленном по длине пластины;

— коэффициент сопротивления турбулентного трения пластины при числе Рейнольдса, вычисленном по длине ламинарного пограничного слоя пластины;

— коэффициент сопротивления ламинарного трения пластины при числе Рейнольдса, вычисленном по длине ламинарного пограничного слоя пластины;

— безразмерная координата точки перехода ламинарного пограничного слоя в турбулентный (безразмерная длина участка ламинарного пограничного слоя).

30. Понятие пограничного слоя и его характеристики.

31. Местное напряжение трения. Коэффициент трения плоской пластины.

32. Отрыв пограничного слоя.

33. Парадокс Даламбера-Эйлера. Сопротивление давления.

5.1. Пластина обтекается потоком при нулевом угле атаки. Определить силу сопротивления пластины при турбулентном пограничном слое, если длина пластины (размер, параллельный потоку) равна 3 м, ширина пластины (размер, перпендикулярный потоку) 16 м, скорость потока 25 м/с при плотности воздуха 1,1 кг/м3 и кинематической вязкости 1,58×10 -5 м2/c.

5.2. Определить толщину пограничного слоя на конце плоской пластины, если длина пластины равна 3 м, скорость потока равна 15 м/c, при кинематической вязкости 1,46×10 -5 м2/c.

5.3. Определить полный коэффициент сопротивления трения пластины, если число Рейнольдса, вычисленное по длине пластины, равно 6×105, а коорди-ната точки перехода ламинарного течения в турбулентное равна 8% от длины пластины.

Глава 6. Аэродинамические характеристики профиля

Изучить материал [1, гл. 6, с. 120 – 143].

— несущие свойства профиля в линейном диапазоне изменения угла атаки

где — частная производная коэффициента подъемной силы профиля от угла атаки;

— профильное сопротивление (сопротивление профиля)

где — коэффициент, учитывающий толщину профиля;

— коэффициент, учитывающий сжимаемость среды;

— коэффициент момента профиля

;

— безразмерная координата фокуса профиля

;

— теорема Жуковского о подъемной силе профиля (для единицы длины)

34. Понятие аэродинамических характеристик.

35. Диаграмма распределения давления по профилю.

36. Критическое число Маха. Волновое сопротивление.

37. Профильное сопротивление.

38. Аэродинамические характеристики профиля.

39. Аэродинамическое качество профиля. Центр давления и фокус профиля.

40. Зависимости коэффициентов подъемной силы и лобового сопротивления от числа Маха.

41. Теорема Жуковского о подъемной силе профиля.

6.1. Определить угол атаки начала отрыва потока на профиле, если коэффициент подъемной силы начала отрыва равен 0,80, частная производная коэффициента подъемной силы по углу атаки равна 0,105 1/град, угол атаки нулевой подъемной силы равен минус 3 градуса.

6.2. Определить коэффициент профильного сопротивления крыла бесконечного размаха с хордой 4,3 м при скорости 470 км/ч на высоте 3000 м, если коэффициент, учитывающий толщину профиля равен 1,24. Пограничный слой считать турбулентным.

6.3. Определить коэффициент подъемной силы секции крыла бесконеч-ного размаха с хордой равной 2,4 м, если интенсивность присоединенного вихря равна 6 м2/с при скорости потока 20 м/с.

Глава 7. Аэродинамические характеристики крыла

Изучить материал [1, гл. 7, с. 144 – 169].

где — поправка, учитывающая влияние формы крыла в плане на угол скоса потока; для наивыгоднейшего крыла ;

— коэффициент индуктивного сопротивления

;

— коэффициент «отвала» поляры

где — поправка, учитывающая влияние формы крыла в плане на «отвал» поляры; для наивыгоднейшего крыла ;

— несущие свойства крыла в линейном диапазоне изменения угла атаки

;

— параболическая поляра крыла

;

— аэродинамическое качество крыла

42. Геометрические характеристики крыла.

43. Вихревая схема крыла конечного размаха.

44. Сила и коэффициент индуктивного сопротивления.

45. Уравнение зависимости для крыла.

46. Уравнение поляры крыла.

47. Аэродинамические характеристики стреловидного крыла.

48. Аэродинамические характеристики крыла малого удлинения.

7.1. Определить средний угол [в градусах] скоса потока в полете у наивыгоднейшего крыла, размахом 28 м, создающего подъемную силу 600 кн при скорости полета 580 км/ч и плотности воздуха 1,2 кг/м3.

7.2. Наивыгоднейшее крыло обтекается потоком со скоростью 600 км/ч при плотности 0,2 кг/м3. Определить аэродинамическое качество наивыгоднейшего крыла, если нагрузка на крыло равна 3000 н/ м2, удлинение крыла равно 6, а коэффициент профильного сопротивления равен 0,009.

7.3. Определить максимальное аэродинамическое качество наивыгоднейшего крыла, если удлинение крыла равно 9, а коэффициент профильного сопротивления равен 0,008 .

Глава 8. Аэродинамические характеристики оперения и рулей

Изучить материал [1, гл. 8, с. 169 – 181].

— несущие свойства профиля с отклоненным рулем

где — коэффициент относительной эффективности руля;

— угол отклонения руля;

— поляра профиля с отклоненным рулем

;

49. Распределение давления по профилю с отклоненным рулем.

50. Эффективность, коэффициент относительной эффективности руля.

51. Зависимость для горизонтального оперения.

52. Уравнение поляры горизонтального оперения.

54. Аэродинамическая компенсация.

8.1. Определить подъемную силу горизонтального оперения (ГО), при угле атаки 1 градус и угле отклонения руля высоты 4 градуса, если площадь го равна 20 м2, площадь руля равна 8 м2, частная производная коэффициента подъемной силы по углу атаки равна 0,09 1/град, скорость потока равна 500 км/ч при плотности 0,3 кг/ м3.

8.2. В потоке на горизонтальном оперении, установленном под нулевым углом атаки, для получения подъемной силы отклонили руль высоты на 6 градусов. Определить, какой угол атаки должно иметь го при неотклоненном руле, чтобы получить такую же подъемную силу, если площадь го равна 32 м2, а площадь руля равна 14 м2.

8.3. При заходе на посадку угол атаки го равен минус 7 градусов. На какой угол надо отклонить руль высоты, чтобы уменьшить подъемную силу го до нуля, если площадь го равна 15,8 м2, а площадь руля высоты равна 5,7 м2.

8.4. Площадь го равна 18 м2, а максимальный угол отклонения руля высоты равен ± 20 градусов. Какую площадь должен иметь руль высоты, чтобы уравновесить силу от заклиненного го на угле минус 10 градусов? Принять 10%-ный запас по углу отклонения руля.

Глава 9. Механизация

Изучить материал [1, гл. 9, с. 182 – 191].

— коэффициенты подъемной силы и профильного сопротивления при выпуске закрылка

; ,

где и — приращения соответствующих коэффициентов при выпуске закрылка

— приращение угла нулевой подъемной силы при выпуске закрылка

55. Виды механизации крыла.

56. Аэродинамические характеристики крыла с отклоненной механизацией.

57. Влияние близости земли на аэродинамические характеристики крыла.

9.1. Крыло в потоке имеет угол нулевой подъемной силы минус 1 градус, угол атаки 4 градуса и коэффициент подъемной силы 0,3. Определить коэффициент подъемной силы при выпущенных закрылках, если угол нулевой подъемной силы стал минус 5 градусов.

9.2. Крыло в потоке имеет угол нулевой подъемной силы 0,9 градуса, угол атаки 5 градусов и коэффициент подъемной силы 0,4. Определить угол атаки нулевой подъемной силы, если при выпущенных закрылках коэффициент подъемной силы стал равным 1,2.

Читайте так же: Чем просверлить металлическую трубу под скважинный адаптер

9.3. При массе 40 т и площади крыла 150 м2 самолет с выпущенными закрылками имеет минимальную скорость 190 км/ч. Какова будет минимальная скорость [км/ч] при отказе выпуска закрылков, если приращение коэффициента подъемной силы при выпуске закрылков равно 0,5.

Глава 10. Аэродинамические характеристики тел вращения

Изучить материал [1, гл. 10, с. 192 – 198].

— коэффициент лобового сопротивления для тела вращения при нулевом угле атаки можно считать равным коэффициенту его профильного сопротивления:

где — коэффициент профильного сопротивления;

— коэффициент сопротивления трения эквивалентной пластины;

— коэффициент, учитывающий удлинение, то есть переход от плоской пластины к телу вращения;

— коэффициент, учитывающий сжимаемость среды;

— смоченная площадь фюзеляжа.

— площадь миделевого сечения.

58. Распределение давления по телу вращения.

59. Аэродинамические характеристики тел вращения при нулевом угле атаки.

10.1. Фюзеляж диаметром 2,8 м, длиной 22 м обтекается потоком со скоростью 600 км/ч. Определить коэффициент лобового сопротивления фюзеляжа, если «смоченная» площадь равна 174 м2, кинематическая вязкость равна 2×10 — 5 м2/с, а коэффициенты, учитывающие удлинение фюзеляжа и сжимаемость, соответственно равны 1,1 и 1,08.

10.2. Фюзеляж диаметром 3 м, длиной 20 м обтекается потоком со скоростью 700 км/ч при кинематической вязкости 2,1×10 — 5 м2/c. Определить коэффициент сопротивления давления фюзеляжа, если “смоченная” площадь равна 158 м2, а коэффициент лобового сопротивления фюзеляжа равен 0,09.

10.3. В модификации самолета геометрически подобно увеличили удлинение фюзеляжа до 11 (=1,09) вместо 7,5 (=1,15) при том же диаметре фюзеляжа, равном 3 м. Как изменится профильное сопротивление фюзеляжа при скорости 680 км/ч на высоте 9000 м?

Глава 11. Аэродинамические характеристики воздушных винтов

Изучить материал [1, гл. 11, с. 198 – 214].

— относительная поступь винта (число Струхаля)

где — диаметр винта;

— число оборотов винта [1/c];

;

— коэффициент полезного действия (КПД) винта

;

— характеристика режима работы несущего винта

где — угловая скорость вращения несущего винта;

— радиус несущего винта;

— коэффициент тяги несущего винта

где — ометаемая площадь несущего винта;

— коэффициент крутящего момента несущего винта

60. Аэродинамические коэффициенты и КПД самолетного винта.

61. Серийная диаграмма винтов.

62. Косая обдувка несущего винта. Маховое движение лопастей.

63. Характеристика режима работы несущего винта.

64. Аэродинамические силы и коэффициенты для несущего винта.

11.1. Самолет массой 20 т при скорости полета340 км/ч имеет аэродинамическое качество 16. Найти КПД винта, если суммарная мощность двигателей на этой скорости 1447 кВт.

11.2. Самолет в потоке с плотностью 0,6 кг/м3 имеет мощность одного двигакВт. Определить его скорость полета [км/ч], если диаметр винта равен 4 м, коэффициент тяги равен 0,064, коэффициент мощности равен 0,08, а КПД равен 0,68.

11.3. Вертолет массой 49 т висит вблизи земли на высоте H » 0. Определить коэффициент тяги несущего винта, если его диаметр равен 32 м, а число оборотов равно 120 об/мин.

11.4. Определить коэффициент крутящего момента несущего винта вертолета, висящего вблизи земли, если его диаметр 29 м, число оборотов равно 126 об/мин, а крутящий момент равен 1100 кНм.

Глава 12. Аэродинамические характеристики самолета

Изучить материал [1, гл. 12, с. 215 – 242].

— учет интерференции в коэффициенте профильного сопротивления

где — коэффициент интерференции для сопротивления;

— подфюзеляжная площадь крыла;

— учет интерференции в коэффициенте «отвала» параболической поляры

где — эффективное удлинение крыла;

— математическое описание несущих свойств самолета в линейном диапазоне зависимости от угла атаки

;

— математическое описание параболической поляры самолета

где — профильное сопротивление;

— наивыгоднейший коэффициент подъемной силы для параболической поляры

;

— максимальное аэродинамическое качество для параболической поляры

65. Аэродинамическая интерференция.

66. Влияние интерференции крыла и фюзеляжа на подъемную силу.

67. Влияние интерференции крыла и фюзеляжа на сопротивление.

68. Влияние балансировки на аэродинамические характеристики.

69. Математическое описание модели несущих свойств самолета на различных режимах полета.

70. Математическое описание модели поляры самолета на различных режимах полета.

71. Влияние упругих деформаций на аэродинамические характеристики.

12.1. Изолированные крыло и фюзеляж имеют коэффициенты профильного сопротивления соответственно 0,01 и 0,15. Определить коэффициент профильного сопротивления комбинации крыла с фюзеляжем (низкоплан), если подфюзеляжная площадь крыла составляет 21 %, а площадь миделя фюзеляжа — 11 % от площади крыла.

12.2. Самолет с массой 140 т и площадью крыла 260 м2 летит со скоростью 840 км/ч при плотности 0,32 кг/м3. Определить коэффициент подъемной силы крыла с учетом балансировки, если коэффициент подъемной силы горизонтального оперения равен 0,4 при его отрицательном угле атаки и площади, составляющей 23 % от площади крыла.

12.3. Самолет с массой 120 т и площадью крыла 254 м2 летит с приборной скоростью 400 км/ч при плотности 0,44 кг/м3. Определить аэродинамическое качество самолета, если коэффициент сопротивления при нулевой подъемной силе равен 0,019, а эффективное удлинение равно 6.

12.4. Самолет с массой 75 т и площадью крыла 170 м2 имеет частную производную коэффициента подъемной силы по углу атаки, равную 0,087 1/град, и летит при плотности 0,66 кг/м3. Определить приращение угла атаки самолета, если его скорость изменится с 900 до 600 км/ч.

12.5. Самолет в горизонтальном полете на высоте 1000 м летит со скоростью 600 км/ч. Определить истинную воздушную скорость [км/ч] при полете на высоте 7000 м, при постоянной приборной скорости.

12.6. Самолет массой 100 т, с площадью крыла 180 м2 летит со скоростью 750 км/ч при плотности 0,414 кг/м3. Определить его максимальное аэродинамическое качество, если коэффициент лобового сопротивления и коэффициент отвала поляры соответственно равны 0,043 и 0,052. Поляру самолета считать квадратичной.

Глава 13. Влияние аэродинамических характеристик

на безопасность полетов

Изучить материал [1, гл. 13, с. 97 – 105].

В процессе летной эксплуатации, чтобы самолет не попал в режим сваливания, необходимо, чтобы полетный (безопасный) коэффициент подъемной силы был меньше коэффициента подъемной силы сваливания.

Это условие задается ограничениями на скорости полета, которые обычно учитываются коэффициентами запаса в зависимости от режима полета:

— взлет ;

— крейсерский полет, посадка .

72. Ограничение коэффициента подъемной силы самолета для недопущения сваливания.

73. Влияние эксплуатационных условий (в аэродинамическом аспекте) на безопасность полетов для самолетов.

13.1. Самолет при нагрузке на крыло 4000 Па летит со скоростью 700 км/ч при плотности 0,3 кг/м3. Определить минимальное значение коэффициента подъемной силы сваливания для обеспечения безопасности полетов.

13.2. Самолет массой 90 т, с площадью крыла 164 м2 летит при плотности 0,34 кг/м3. Определить его минимально-допустимую скорость сваливания [км/ч], если крейсерский коэффициент подъемной силы при этом равен 0,45.

Глава 14. Влияние аэродинамических характеристик

на экономичность полетов

Изучить материал [1, гл. 14, с. 253 – 258].

Экономичность полетов определяется общепризнанным критерием — топливной экономичностью полетов, показывающим массовый расход топлива в граммах, приходящийся на единицу транспортной работы.

Топливная эффективность полетов определяется по формулам

— для самолетов с реактивными двигателями

; ;

— для самолетов с винтовыми двигателями

; ,

где — удельный расход топлива для ДТРД — кг/(Н×ч), для ТВД — кг/(квт×ч);

— коммерческая отдача самолета; ;

— КПД винта.

74. Транспортная работа и единицы ее измерения. Топливная эффективность полета (ТЭП).

75. Влияние эксплуатационных условий (в аэродинамическом аспекте) на топливную эффективность полета для самолетов.

14.1. Определить топливную эффективность полета самолета на один пассажиро-километр, имеющего удельный расход топлива 0,0643 кг/(нч), коэффициенты подъемной силы и лобового сопротивления соответственно 0,42 и 0,033, коммерческую отдачу 0,18 при скорости 650 км/ч.

14.2. Самолет в крейсерском полете имеет коммерческую отдачу 0,17, аэродинамическое качество 14 и удельный расход топлива 0,0587 кг/(нч). Определить топливную эффективность полета самолета на один пассажиро ‑ километр, если скорость сваливания на этом режиме равна 500 км/ч.