В изогнутой трубе расположенной в вертикальной плоскости
В вертикальной плоскости расположена гладкая трубка, изогнутая периодически в виде дуг окружностей одинаковым радиусом R (см. рис.). В верхнее отверстие трубки без начальной скорости запускают шарик массой m = 10 г. С какой по модулю силой F шарик действует на трубку в точке А, в конце первой половины периода своего движения по трубке?
Как видно из рисунка, к концу первого полупериода движения по трубке шарик опустится по высоте на расстояние Поскольку потерь механической энергии нет (по условию трубка гладкая), то скорость шарика к этому моменту будет равна
В точке A шарик движется по окружности с центростремительным ускорением, равным которое, согласно второму закону Ньютона, создаётся нормальной силой давления со стороны трубки:
По третьему закону Ньютона эта сила по модулю равна искомой силе давления шарика на трубку: Н.
| Критерии оценивания выполнения задания | Баллы | |
|---|---|---|
| Приведено полное решение, включающее следующие элементы: I) записаны положения теории и физические законы, закономерности, применение которых необходимо для решения задачи выбранным способом (в данном случае: закон сохранения механической энергии, закон сохранения импульса); II) описаны все вновь вводимые в решении буквенные обозначения физических величин (за исключением обозначений констант, указанных в варианте КИМ, и обозначений величин, используемых в условии задачи); III) проведены необходимые математические преобразования, приводящие к правильному ответу; IV) представлен правильный ответ | 3 | |
| Правильно записаны все необходимые положения теории, физические законы, закономерности, и проведены необходимые преобразования. Но имеются следующие недостатки. Записи, соответствующие пункту II, представлены не в полном объёме или отсутствуют. В решении лишние записи, не входящие в решение (возможно, неверные), не отделены от решения (не зачёркнуты; не заключены в скобки, рамку и т.п.). В необходимых математических преобразованиях или вычислениях допущены ошибки, и (или) преобразования/вычисления не доведены до конца. Отсутствует пункт IV, или в нём допущена ошибка | 2 | |
| Представлены записи, соответствующие одному из следующих случаев. Представлены только положения и формулы, выражающие физические законы, применение которых необходимо для решения задачи, без каких-либо преобразований с их использованием, направленных на решение задачи, и ответа. В решении отсутствует ОДНА из исходных формул, необходимая для решения задачи (или утверждение, лежащее в основе решения), но присутствуют логически верные преобразования с имеющимися формулами, направленные на решение задачи. Задание Д1 Тарг 1983 гЗадача Д1 Внимание! Номер рисунка выбирается по предпоследней цифре варианта Номер условия в таблице — по последней цифре варианта Решение. Пример выполнения задания Д1
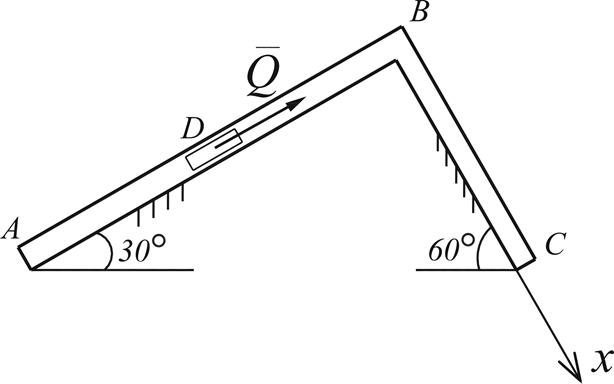
Пример выполнения задания Д1. Условие задачи: Тело массой m = 2 кг, получив в точке A начальную скорость V0 = 8 м/с, движется в изогнутой трубке АВС, расположенной в вертикальной плоскости. На участке AB на тело кроме силы тяжести действует, как указано на рис. Д1.2, постоянная сила Q = 9,8 Н и сила сопротивления R = 0,5 V 2 Н. Пройдя расстояние AB = l = 3 м, тело D в точке B, не изменяя значения своей скорости, переходит на участок ВС трубы, где на него кроме силы тяжести действует переменная сила, проекция которой на ось Х равна Fx = 8t + 4cos0,2t (Н) и сила трения скольжения. Коэффициент трения скольжения f = 0,1. Найти закон движения тела D на участке ВС. Принять g = 9,8 м/с 2 . Запишем условие задачи в кратком виде: Определить: х = х ( t ). Сила трения по модулю равна:
В выражении (1) ускорение свободного падения Составим дифференциальное уравнение движения материальной точки в проекции на ось Х: Для нахождения искомого закона движения материальной точки необходимо дважды проинтегрировать уравнение (2). Первый интеграл: Произвольные постоянные С1 и С2 определим из начальных на участке ВС условий: при t = 0 начальное положение тела D равно Хо = 0, а начальная его скорость равна VB. Следовательно, подставляя начальные условия в уравнения (3) и (4) получим: Таким образом, искомое уравнение движения тела D на участке ВС принимает вид: Неизвестной величиной в уравнении движения (5) является начальная на участке ВС скорость тела D. По условию задачи «…тело D в точке B, не изменяя значения своей скорости, переходит на участок ВС трубы…», следовательно, начальная скорость тела на участке ВС VB равна по модулю конечной скорости тела VB на участке АВ. Переходим, для нахождения скорости VB, к рассмотрению движения тела D на участке АВ. 2. Рассмотрим движение тела D, которое принимаем за материальную точку, на участке АВ. Изображаем тело в произвольном положении на этом участке и прикладываем действующие на него силы: силу тяжести нормальную реакцию стенки трубки Составим дифференциальное уравнение движения тела D на участке АВ в проекции на ось У: Сократим обе части уравнения (6) на массу m и подставим цифровые параметры: то полученное уравнение (7) принимает вид: Полученное дифференциальное уравнение (8) является уравнением первого порядка с разделяющими переменными. Разделив переменные, имеем: Постоянную интегрирования С3 находим из начальных условий на участке АВ: при t = 0 начальная координата тела D равна у0 = 0 и начальная скорость V0 = VA. Следовательно: Подставив выражение (10) в уравнение (9) получим: Формула (11) – это закон изменения скорости тела D на участке АВ. Подставляем в эту формулу значение длины участка АВ = l = ук = 3 м, найдем скорость тела D в точке В: 3. Определение уравнения движения тела D на участке ВС. Выяснив значение модуля скорости тела D в точке В, подставляем (12) в уравнение (5): Ответ: 4. ЗАДАНИЕ Д2 Применение общих теорем к изучению движения материальной точки Шарик, принимаемый за материальную точку, двигается из положения А в середине трубки, ось которой находится в вертикальной плоскости (рис.Д2.1). Найти скорость шарика в положениях В, С, Д, Е и силу давления шарика на стенку трубки в положении С. Силами трения на криволинейных участках траектории пренебречь. Необходимые для расчетов данные приведены в таблицах Д-2.1 и Д-2.2, в которых:
f — коэффициент трения скольжения шарика на прямолинейных участках трубки; R — радиус кривизны трубки; Указания: 1. По последней цифре номера зачетной книжки следует выбрать схему, что изображена на рис. Д2.1. 2. По предпоследней цифре номера зачетной книжки следует выбрать параметры для расчета, которые представлены в табл. Д-2.1 и Д-2.2. Adblockdetector |






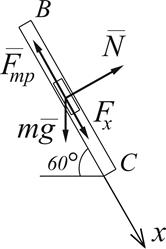 1. Считая тело D материальной точкой, рассмотрим его движение на участке ВС (ось Х уже выбрана). На тело D действуют (рис. Д1.3): сила тяжести
1. Считая тело D материальной точкой, рассмотрим его движение на участке ВС (ось Х уже выбрана). На тело D действуют (рис. Д1.3): сила тяжести 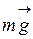 , нормальная реакция стенки трубки
, нормальная реакция стенки трубки 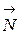 , переменная сила, проекция которой на ось Х равна
, переменная сила, проекция которой на ось Х равна 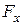 и сила трения
и сила трения 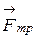 .
.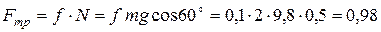 Н. (1)
Н. (1)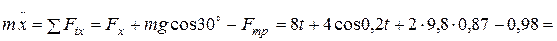
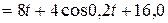 (Н).
(Н).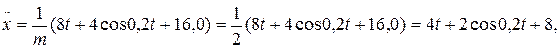 м/c 2 . (2)
м/c 2 . (2)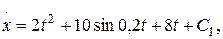 (3)
(3)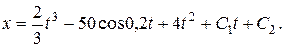 (4)
(4)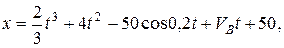 м. (5)
м. (5)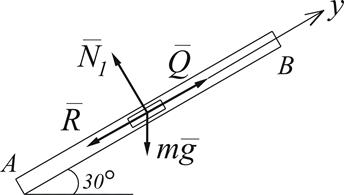
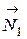 , силу
, силу 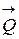 и силу сопротивления
и силу сопротивления 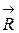 . Здесь же показана и выбранная система координат – ось У. Ось одна, т.к. на участке АВ, так же как и на участке ВС, тело D движется прямолинейно.
. Здесь же показана и выбранная система координат – ось У. Ось одна, т.к. на участке АВ, так же как и на участке ВС, тело D движется прямолинейно.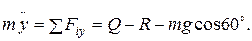 (6)
(6)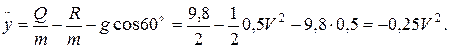 (7)
(7)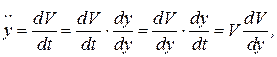
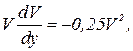
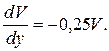 (8)
(8)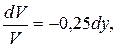
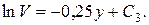 (9)
(9)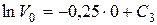
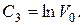 (10)
(10)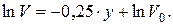
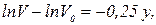
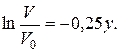
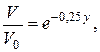
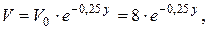 м/с. (11)
м/с. (11)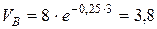 м/с. (12)
м/с. (12)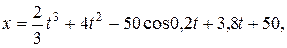 м.
м.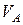 — скорость шарика в положении А;
— скорость шарика в положении А;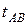 — время движения шарика на участке АВ;
— время движения шарика на участке АВ;
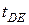 — время движения шарика на участке DЕ;
— время движения шарика на участке DЕ;