Динамическая вязкость воздуха в трубе

Сведения о вязкости

Вязкость – свойство газов и жидкостей оказывать сопротивление необратимому перемещению одной их части относительно другой при сдвиге, растяжении и других видах деформации.

Различают динамическую (или абсолютную) вязкость и кинематическую вязкость.

Динамическая (абсолютная) вязкость µ – сила, действующая на единичную площадь плоской поверхности, которая перемещается с единичной скоростью относительно другой плоской поверхности, находящейся от первой на единичном расстоянии.

В системе СИ динамическая вязкость выражается в Па⋅с (паскаль-секунда), внесистемная единица П (пуаз).

Соотношение величин динамической вязкости в различных единицах измерения

Единицы измерения	Па⋅с	сП	П	кгс⋅с/м 2	Н⋅с/м 2	дин⋅с/cм 2	г/(см⋅с)
1 Па⋅с паскаль-секунда	1	1000	10	0,102	1	10	10
1 сП сантипуаз	0,001	1	0,01	0,0001	0,001	0,01	0,01
1 П пуаз	0,1	100	1	0,01	0,1	1	1
1 кгс⋅с/м 2 килограмм-сила-секунда на квадратный метр	9,81	9806,7	98,07	1	9,81	98,07	98,07
1 Н⋅с/м 2 ньютон-секунда на квадратный метр	1	1000	10	0,102	1	10	10
1 дин⋅с/см 2 дина-секунда на квадратный сантиметр	0,1	100	1	0,01	0,1	1	1
1 г/(см⋅с) грамм на сантиметр на секунду	0,1	100	1	0,01	0,1	1	1

Кинематическая вязкость ν – отношение динамической вязкости µ к плотности жидкости ρ.

где:
ν, м 2 /с – кинематическая вязкость;
μ, Па⋅с – динамическая вязкость;
ρ, кг/м 3 – плотность жидкости.

В системе СИ кинематическая вязкость выражается в м 2 /с (квадратный метр в секунду), внесистемная единица Ст (стокс).

Соотношение величин кинематической вязкости в различных единицах измерения

Источник

Расчет потерь напора в водопроводных трубах, вентиляционных каналах, речных руслах

Поток воды, воздуха бывает ламинарным (т.е. спокойным, плавным, безвихревым) и турбулентным (завихренным). При малых скоростях потока движение ламинарно. При больших скоростях — турбулентно. Сопротивление движению в трубах при ламинарном характере намного меньше, чем при турбулентном. (В авиации, при внешнем обтекании крыльев и фюзеляжа картина обратная.). Граница перехода ламинарного течения в турбулентное определяется критическим числом Рейнольдса.

Для жидкости и воздуха формулы совершенно одинаковы. И совершенно неважно какие размеры потока. Прохождение потока воздуха по трубочке 5 мм диаметром, подающей воздух в аквариум, и течение Волги с километровой шириной русла подчиняются одним и тем же законам гидродинамики.

Для произвольной формы канала, по которому движется поток, число Рейнольдса равно:

v — скорость потока м/с
A — площадь потока м 2 ,
l — смоченный периметр м,
ν — кинематическая вязкость м 2 /с,
для воздуха ν = 0,000 014 м 2 /с,
для воды ν = 0,000 001 м 2 /с,
R_G — гидравлический радиус равный отношению площади потока к смоченному периметру м.

Критическое число Рейнольдса, при котором ламинарный поток переходит в турбулентный, равно 239.

Для квадратных, полностью заполненных, труб число Рейнольдса равно:

Для прямоугольных, полностью заполненных, труб число Рейнольдса равно:

Критические числа для квадратных и прямоугольных труб также равны 239.

Для круглых полностью заполненных труб число Рейнольдса другое :

При расчете числа Рейнольдса для круглых труб чаще всего подставляется не гидравлический радиус, а диаметр трубы, который в 4 раза больше гидравлического радиуса

Для избежания недоразумений необходимо знать какой характерный размер использовался для вычисления. Если в формулы подставляли гидравлический радиус, то надо надо сравнивать вычисленное значение Re с 239, а если подставляли диаметр круглой трубы, сторону прямоугольной трубы или диагональ, то критическое число будет 956.

Необходимо добавить, что число Рейнольдса довольно «размытый» показатель. На процессы турбулентности сильно влияют наличие первоначальной завихренности потока, шероховатость поверхности, форма тела, взаимодействующая с потоком. Поэтому указанные критические числа Рейнольдса равные 956 для круглых заполненных труб и 239 для остальных случаев не слишком точны. В литературе можно встретить значения, отличающиеся от приведенных, в 2 раза.. Кроме того существует широкая переходная область между ламинарным и турбулентным течением без четко выраженной границы, поэтому фиксация точки перехода во многом зависит от индивидуальности экспериментатора.

В программе для вычисления потерь напора для круглых труб подстваляется диаметр, а в остальных случаях, в отличие от методики Теплова, учетверенный гидравлический радиус. Это сделано для того, чтобы критическое число Рейнольдса во всех случаях получалось одиноково и равно 956.

Сопротивление движению жидкости для ламинарного течения пропорционально скорости движения потока, а для турбулентного течения пропорционально квадрату скорости движения. При турбулентном течении сопротивление в каналах с увеличением скорости растет значительно быстрее.

Падение давления в круглой трубе для ламинарного потока согласно формуле Пуазейля при Re

Δp — падение давления Па,
v — скорость потока м/с,
η — динамическая вязкость Па•с,
для воздуха η = 0,000 0182 Па•с,
для воды η = 0,001 Па•с,
L — длина трубы м,
D — диаметр трубы м,
Q — расход м 3 /с.

Скорость потока и расход связаны соотношением

Q — расход м 3 /с,
v — скорость потока м/с,
A — площадь потока м 2 .

Профессор А. В. Теплов в своей книге «Основы гидравлики» пишет, что с середины 19 века было предложено несколько сотен эмпирических формул для расчета сопротивления потоку. Приведенные здесь формулы разработаны профессором А. В. Тепловым в результате обработки экспериментальных данных. В формулах учитывается число Рейнольдса и шероховатость каналов. Ответственные, официальные расчеты предписывается считать по методике соответствующих ГОСТов, поэтому данная методика подходит для ориентировочных расчетов.

Падение давления в круглой полностью заполненной трубе для турбулентного потока при Re>Reкр.

Падение давления в трубе или русле произвольной формы для турбулентного потока при Re>Reкр. :

Δp — падение давления Па
ρ — плотность кг/м 3
для воздуха ρ = 1,29 кг/м 3 ,
для воды ρ = 1000 кг/м 3 ,
v — скорость потока м/с,
ν — кинематическая вязкость м 2 /с,
для воздуха ν = 0,000 014 м 2 /с,
для воды ν = 0,000 001 м 2 /с,
L — длина канала м,
D — диаметр трубы м,
Q — расход м 3 /с
Δ — шероховатость м
R_G = A/S — гидравлический радиус м.

Значения шероховатости Δ по проф. А. В. Теплову

Очень гладкие поверхности 0, 000 1 м
Тщательно остроганные доски, чистая штукатурка, стеклянные, латунные, медные, свинцовые и новые стальные трубы 0, 000 1 — 0, 000 2 м
Штукатурка, деревянные, бетонные, асбоцементные, и новые чугунные трубы 0, 000 2 — 0, 000 5 м
Нестроганые доски, стальные и чугунные б/у трубы, бетонные стенки 0. 000 5 — 0, 001 м
Хорошая кладка, клепаные трубы, канализационные трубы 0, 001 — 0, 002 м
Средняя кирпичная кладка, асфальтовая мостовая 0,002 — 0,005 м
Бутовая кладка, булыжная мостовая 0,005 — 0,01 м
Земляные каналы с хорошим содержанием 0,02 — 0,05 м
Реки 0,1 — 0,2 м
Реки с камнями, с водорослями более 0,2 м

Зависимость динамической и кинематической вязкости от температуры и давления.

Динамическая и кинематическая вязкозть связаны множителем плотности:

ν — кинематическая вязкость м 2 /с,
для воздуха ν = 0,000 0133 м 2 /с,
для воды ν = 0,000 00179 м 2 /с,
η — динамическая вязкость Па•с,
для воздуха η = 0,000 0172 Па•с,
для воды η = 0,00178 Па•с,
ρ — плотность кг/м 3
для воздуха ρ = 1,29 кг/м 3 ,
для воды ρ = 1000 кг/м 3

Параметры даны для атмосферного давления при температуре 0 градусов Цельсия.

Динамическая вязкость воды практически не зависит от давления и нелинейно уменьшается при росте температуры. Табличные величины динамической вязкости до температуры 350 градусов Цельсия я нашел по адресу chillers.ru. Эти табличные величины можно аппроксимировать следующими формулами:

Где t — температура в градусах Цельсия.

График зависимости динамической и кинематической вязкости воды от температуры

Плотность воды с увеличением температуры падает по закону

ρ— плотность кг/м 3 ,
t — температура по Цельсию

Динамическая вязкость воздуха сильно зависит от температуры и давления. При повышении давления увеличивается плотность воздуха, поэтому кинематическая вязкозть, получаемая делением динамической вязкозти на плотность очень сильно падает с увеличением температуры.

В книге Нестеренко А. В. Основы термодинамических расчетов вентиляции и кондиционирования воздуха МВШ 1971 г. приводится формула динамической вязкости для воздуха

t — температура по Цельсию
g = 9,81 м/с 2 ,
для воздуха μ₀ = 174·10 -8 с = 114,
для пара μ₀ = 90,2·10 -8 с = 673.

На сайте www.dpva.info приведена таблица зависимости параметров воздуха от давления и температуры. График динамической вязкости построен по данным этой таблицы.

График зависимости динамической и кинематической вязкости воздуха от давления и температуры

Этот график довольно точно аппроксимируется линейными уравнениями. Ошибка не превышает 2%.

Для вычисления кинематической вязкости необходимо знать плотность воздуха. Плотность газа рассчитывается по известному закону Клайперона:

ρ— плотность кг/м 3 ,
p — абсолютное давление Па,
R — газовая постоянная 287 Дж/(кгК)
t — температура по Цельсию.

p — абсолютное давление Па,
t — температура по Цельсию.

29 ноября 2009 г.
Розин М.Н.

Источник

Динамическая вязкость газов и паров

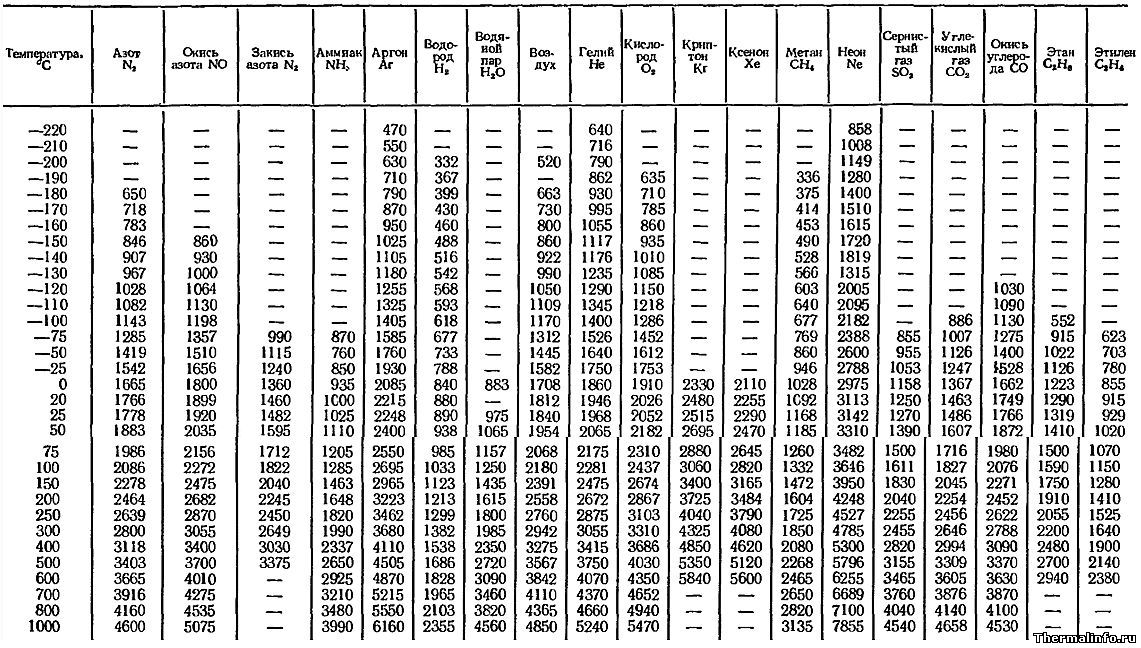
Динамическая вязкость газов и паров в интервале температуры от -220 до 1000°С

В таблице представлена динамическая вязкость газов и паров в зависимости от температуры (при отрицательной и положительной температуре).

Динамическая вязкость газов в таблице выражена в Па·сек с множителем 10 -8 . Например, коэффициент динамической вязкости азота N₂ при нормальных условиях (при температуре 0°С и нормальном атмосферном давлении) равен 1665·10 -8 или 0,00001665 Па·с.

По данным таблицы видно, что наиболее вязким газом при комнатной температуре является газ неон — вязкость неона равна 3113·10 -8 Па·с.

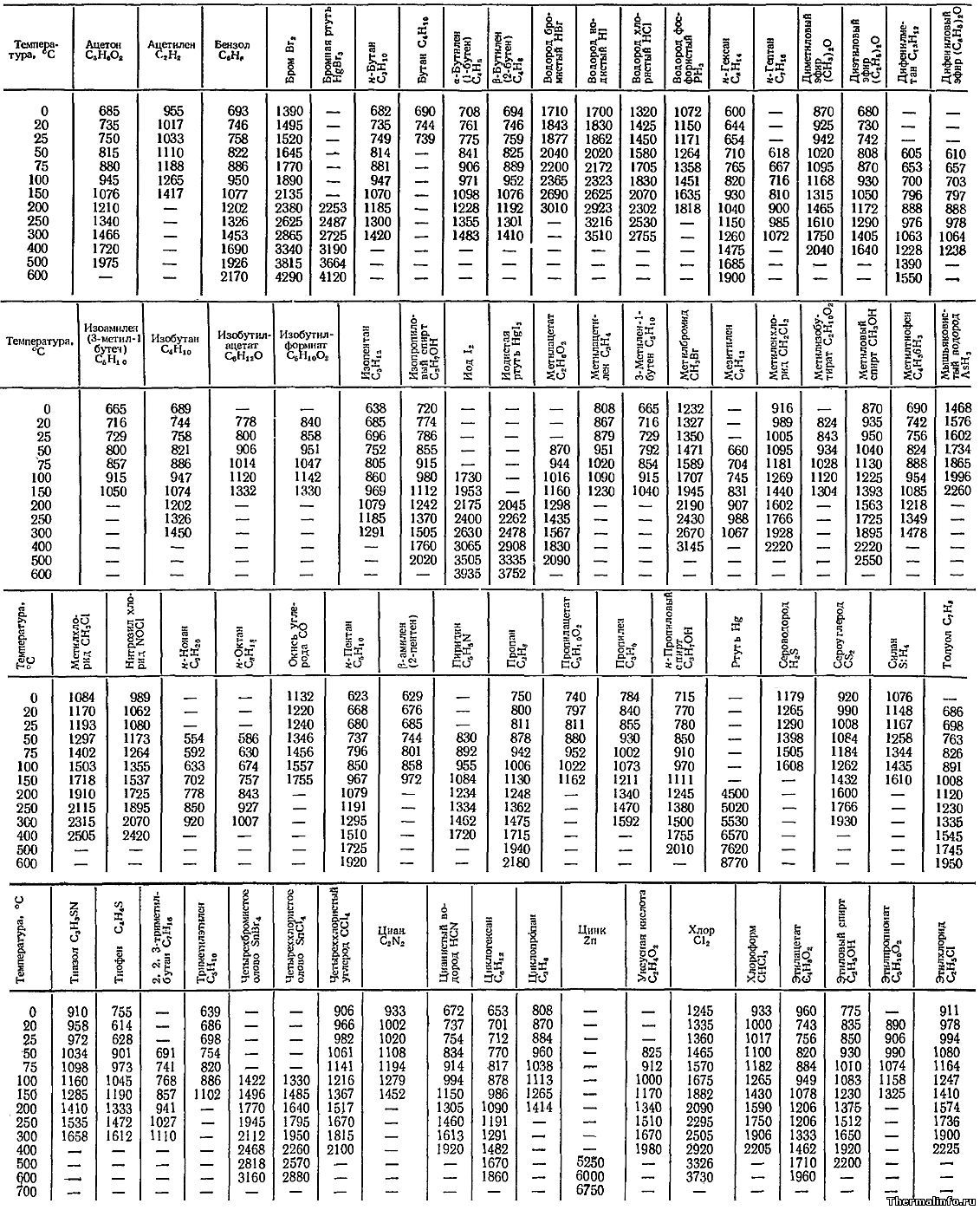
Динамическая вязкость газов и паров в диапазоне температуры от 0 до 700°С

В таблице приведены значения коэффициента динамической вязкости газов и паров при положительной температуре в диапазоне от 0 до 700°С.

Вязкость в таблице выражена в Па·сек с множителем 10 -8 . Например, коэффициент динамической вязкости ацетилена C₂H₂ при нормальных условиях равен 955·10 -8 или 0,00000955 Па·с.

Даны значения динамической вязкости следующих газов и паров: ацетон (диметилкетон, пропанон) C₃H₆O, бензол C₆H₆, бром Br₂, бромная ртуть (бромид ртути III) HgBr₃, n-бутан C₄H₁₀, бутан C₄H₁₀, бутилен (1-бутен) C₄H₈, 2-бутен C₄H₈, водород бромистый (бромоводород) HBr, водород йодистый (иодоводород) HI, водород хлористый (газообразная соляная кислота, хлороводород) HCl, водород фтористый (фтороводород, гидрофторид, фторид водорода) HF, n-гексан (гексан) C₆H₁₄, n-гептан C₇H₁₆, диметиловый эфир (метиловый эфир, метоксиметан, древесный эфир) C₂H₆O, диэтиловый эфир (этиловый эфир, серный эфир) C₄H₁₀O, дифенилметан С₁₃Н₁₂, дифениловый эфир C₁₂H₁₀O, изоаметилен (3-метил-1-бутен) C₅H₁₀, изобутан (метилпропан, 2-метилпропан) С₄Н₁₀, изобутилацетат (изобутиловый эфир уксусной кислоты) С₆Н₁₂О₂, изобутилформиат C₅H₁₀O₂, изопентан C₅H₁₂, изопропиловый спирт (пропанол-2, 2-пропанол), изопропанол, диметилкарбинол) С₃Н₇ОН, иод (йод) I₂, йодистая ртуть HgI₃, метилацетат (метиловый эфир уксусной кислоты) С₃Н₆О₂, метилацетилен (пропин) C₃H₄, 3-метилен-1-бутен C₅H₁₀, метилбромид (бромистый метил, монобромметил, монобромэтан, метилбромид, бромметил) CH₃Br, мезитилен C₉H₁₂, метиленхлорид (хлористый метилен, дихлорметан, ДХМ) CH₂Cl₂, метилизобутират C₂H₁₀O₂, метиловый спирт (метанол, древесный спирт, карбинол, метилгидрат, гидроксид метила) CH₃OH, метилтиофен, мышьяковистый водород (гидрид мышьяка, арсин) AsH₃, метилхлорид (хлорметан) CH₃Cl, нитрозил хлорид (хлористый нитрозил, оксид хлорид азота) NOCl, нонан C₉H₂₀, октан C₈H₁₈, окись углерода CO, н-пентан C₅H₁₂, амилен, пиридин C₅H₅N, пропан C₃H₈, пропилацетат (н-пропиловый эфир уксусной кислоты) C₅H₁₀O₂, пропилен C₃H₆, пропиловый спирт (пропан-1-ол, 1-пропанол) C₃H₇OH, ртуть Hg, сероводород H₂S, сероуглерод CS₂, силан (кремневодород, гидрид кремния) SiH₄, толуол (метилбензол) C₇H₈, тиазол C₃H₃NS, тиофен C₄H₄S, триметилбутан C₇H₁₆, триметилэтилен С₅Н₁₀, четырехбромистое олово (бромид олова IV) SnBr₄, четыреххлористое олово (хлорид олова IV) SnCl₄, четыреххлористый углерод (тетрахлорметан, ЧХУ) CCl₄, циклогексан C₆H₁₂, циклопропан C₃H₆, цинк Zn, уксусная кислота (этановая кислота) C₂H₄O₂, хлор Cl₂, хлороформ (трихлорметан, метилтрихлорид, хладон-20) CHCl₃, этилацетат (этиловый эфир уксусной кислоты) C₄H₈O₂, этиловый спирт (этанол, метилкарбинол, винный спирт или алкоголь C₂H₆O) C₂H₅OH, этилпропионат C₅H₁₀O₂, этилхлорид (хлористый этил, монохлорэтан) C₂H₅Cl.

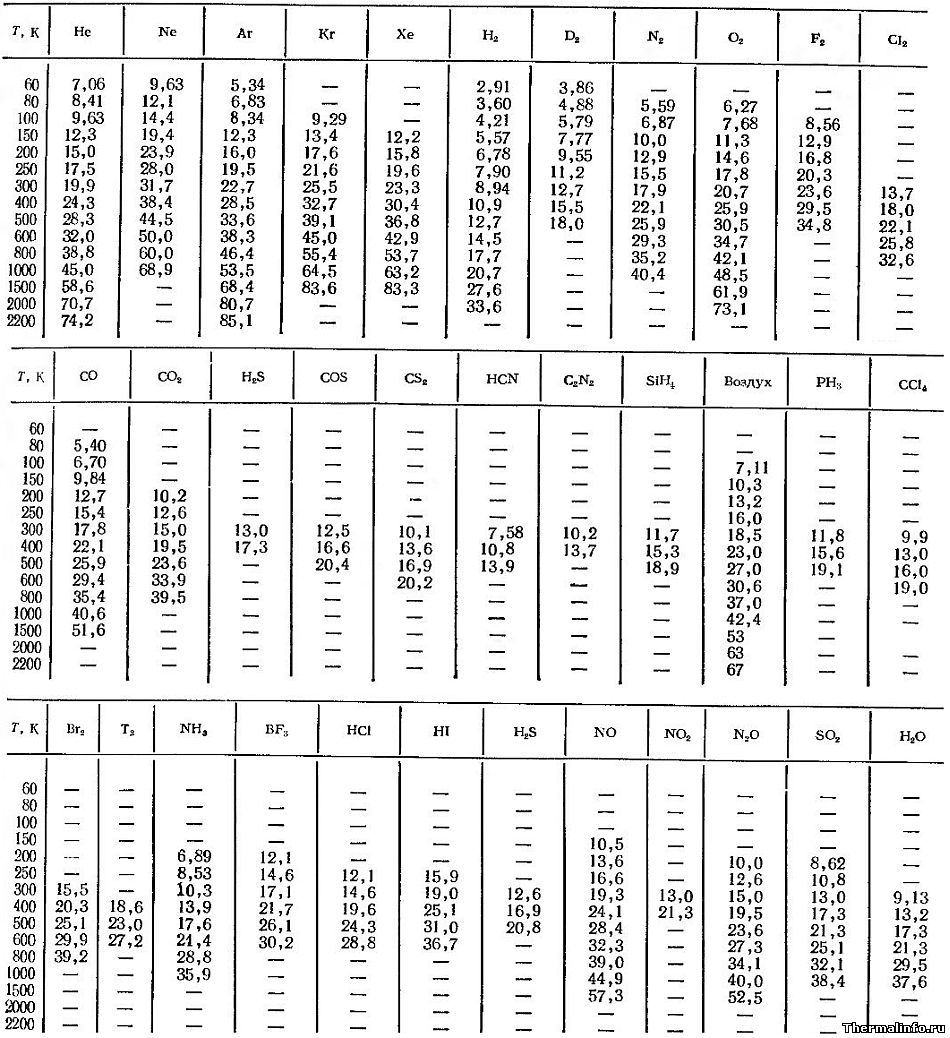
Динамическая вязкость газов при температуре от -213 до 1927°С

В таблице представлены значения коэффициента динамической вязкости газов в зависимости от температуры при атмосферном давлении. Вязкость газов указана при отрицательных от 60К (-213°С) и положительных температурах до 2200К (1927°С).

Вязкость в таблице выражена в Па·сек с множителем 10 -6 . Например, коэффициент динамической вязкости газа аргона при температуре 27°С (300 К) равен 22,7·10 -6 или 0,0000227 Па·с.

В таблице указан коэффициент динамической вязкости следующих газов: гелий He, неон Ne, аргон Ar, криптон Kr, ксенон Xe, водород H₂, дейтерий D₂, азот N₂, кислород O₂, фтор F₂, хлор Cl₂, окись углерода CO, углекислый газ CO₂, сероводород H₂S, углерода оксид-сульфид (сероокись, карбонилсульфид) COS, синильная (циинистоводородная) кислота (цианистый водород) HCN, дициан C₂N₂, силан (кремневодород, гидрид кремния) SiH₄, воздух, фосфин PH₃, четыреххлористый углерод (тетрахлорметан, ЧХУ) CCl₄, бром Br₂, иод I₂, аммиак NH₃, водород хлористый (газообразная соляная кислота, хлороводород) HCl, водород йодистый (йодоводород) HI, окись азота NO, оксид азота NO₂, оксид азота N₂O, сернистый газ SO₂, водяной пар H2O.

Следует отметить, что с ростом температуры значение динамической вязкости газов увеличивается.

1. Таблицы физических величин. Справочник. Под ред. акад. И.К. Кикоина. М.: Атомиздат, 1976. — 1008 с.
2. Физические величины. Справочник. А.П. Бабичев, Н.А. Бабушкина, А.М. Братковский и др.; Под ред. И.С. Григорьева, Е.З. Мейлихова. — М.:Энергоатомиздат, 1991. — 1232 с.

Источник